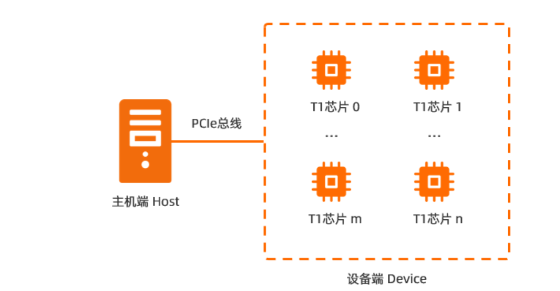
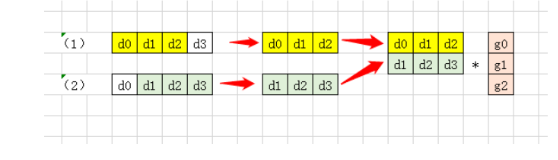
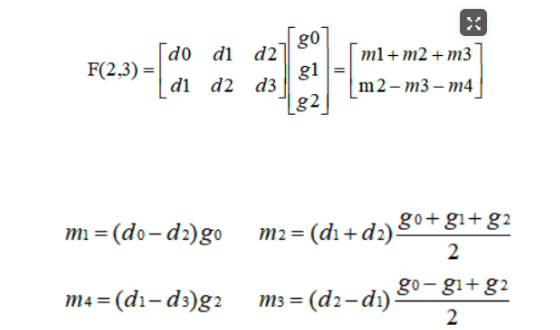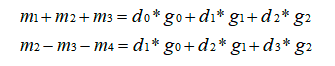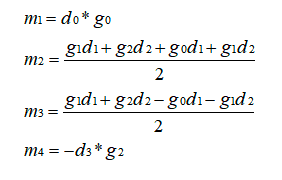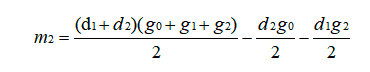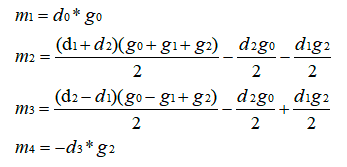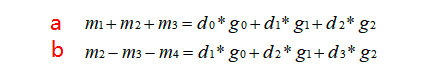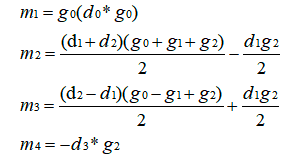循环优化
循环优化整体策略为循环展开、循环合并与循环顺序的交换:
循环展开
通过减少循环迭代次数来降低循环控制开销,将多个迭代步骤合并执行:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
while(i < count){
a[i] = i;
i++;
}
while(i < count - 1){
a[i] = i;
a[i+1] = i+1;
i += 2;
}
if(i == count-1){
a[count-1] = count-1;
}
|
循环合并
对于计数器相同的多个循环,将其合并为一个循环,避免多次轮询:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
for(i = 0; i < index; i++){
do_type_a_work(i);
}
for(i = 0; i < index; i++){
do_type_b_work(i);
}
for(i = 0; i < index; i++){
do_type_a_work(i);
do_type_b_work(i);
}
|
循环顺序交换
计算外提
将循环内不变的计算提取到循环外部,减少无效计算:
1
2
3
4
5
6
|
for(int i = 0; i < get_max_index(); i++){}
int max_index = get_max_index();
for(int i = 0; i < max_index; i++){}
|
多级寻址外提
将循环内的多级指针寻址提取到外部,避免反复寻址跳转:
1
2
3
4
5
6
7
8
9
10
11
12
|
for(int i = 0; i < max_index; i++){
ainfo->bconfig.cset[i].index = index;
ainfo->bconfig.cset[i].flag = flag;
}
set = ainfo->bconfig.cset;
for(int i = 0; i < max_index; i++){
set[i].index = index;
set[i].flag = flag;
}
|
判断外提
将循环内固定不变的条件判断提取到外部,减少比较次数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
for(i = 0; i < index; i++) {
if (type == TYPE_A) {
do_type_a_work(i);
} else {
do_type_b_work(i);
}
}
if (type == TYPE_A) {
for(i = 0; i < index; i++) {
do_type_a_work(i);
}
} else {
for(i = 0; i < index; i++) {
do_type_b_work(i);
}
}
|
循环嵌套顺序调整
将最繁忙的循环放在最内层,提高缓存利用率:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
for (column = 0; column < 100; column++) {
for (row = 0; row < 5; row++) {
sum += table[row][column];
}
}
for (row = 0; row < 5; row++) {
for (column = 0; column < 100; column++) {
sum += table[row][column];
}
}
|
- 充分分解小的循环:要充分利用CPU的指令缓存,就要充分分解小的循环。特别是当循环体本身很小的时候,分解循环可以提高性能。注意:很多编译器并不能自动分解循环。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
for (i = 0; i < 4; i++) {
r[i] = 0;
for (j = 0; j < 4; j++) {
r[i] += M[j][i] * V[j];
}
}
r[0] = M[0][0]*V[0] + M[1][0]*V[1] + M[2][0]*V[2] + M[3][0]*V[3];
r[1] = M[0][1]*V[0] + M[1][1]*V[1] + M[2][1]*V[2] + M[3][1]*V[3];
r[2] = M[0][2]*V[0] + M[1][2]*V[1] + M[2][2]*V[2] + M[3][2]*V[3];
r[3] = M[0][3]*V[0] + M[1][3]*V[1] + M[2][3]*V[2] + M[3][3]*v[3];
|
- 提取公共部分:对于一些不需要循环变量参加运算的任务可以把它们放到循环外面,这里的任务包括表达式、函数的调用、指针运算、数组访问等,应该将没有必要执行多次的操作全部集合在一起,放到一个init的初始化程序中进行。
OpenMP 并行优化策略
- for 循环之前直接加:#pragma omp parallel for 即可自动并行;
- 没有 for 循环,还想让代码并行一起干活就用 sections、section:
1
2
3
4
5
6
7
8
| #pragma omp parallel sections{
#pragma omp parallel section
#pragma omp parallel section
...
}
|
但是这样做有个缺点:如果想让每个人干的活差不多,我们得学怎么分任务,太麻烦也不好实现,很容易划分不佳;并且还有一个问题:同一个 sections 内部,不同的 section 之间变量会不会相互干预?我们一定能找到变量相互干预的情况,也一定能找到变量相互不干预的情况。为了区别不同并行区域之间变量是自己使用,还是给大家共享使用,我们定义不同的类型:
- 私有不干预:private,将变量声明为私有,并行完成后消失,不干预并行区域外的同名变量。
- 继承不干预:firstprivate,并行之前就有这个变量存在,并行完成后区域内消失,外面的变量保持原值。
- 私有干预:lastprivate,并行区域内生成,并行完成后保存在并行外部。
- 复制不干预:threadprivate,共享版 private。
private 子句
1
2
3
4
5
6
| int k = 100;
#pragma omp parallel for private(k)
for ( k=0; k < 10; k++){
printf("k=%d\n", k);
}
printf("last k=%d\n", k);
|
输出结果是:首先是 0-9 的乱序输出(并行没有顺序),其次就是 last k=100,内外不干预,内部 k 虽然不断变化,但外面的 k 仍然保持 100。
firstprivate 子句
private 虽好,但是它不能继承来自外面的同名变量的值,也就是内外不相联系。firstprivate 可以继承外面变量值用以内部使用,但是对外面变量不会有影响:
1
2
3
4
5
6
7
| int k = 100;
#pragma omp parallel for firstprivate(k)
for ( i=0; i < 4; i++){
k+=i;
printf("k=%d\n",k);
}
printf("last k=%d\n", k);
|
打印结果是:k=100-103 之间乱序输出,last k=100。
lastprivate 子句
firstprivate 虽然能从外面继承,但是不能干预外部,只能自娱自乐。lastprivate 能干预外部。
1
2
3
4
5
6
7
| int k = 100;
#pragma omp parallel for firstprivate(k),lastprivate(k)
for ( i=0; i < 4; i++){
k+=i;
printf("k=%d\n",k);
}
printf("last k=%d\n", k);
|
打印结果是:k=100-103 之间乱序输出,last k=103。
threadprivate 子句
threadprivate 子句用来指定全局的对象被各个线程各自复制了一个私有的拷贝,即各个线程具有各自私有的全局对象,通常用来做计数器,
1
2
3
4
5
6
| int counter = 0;
#pragma omp threadprivate(counter)
int increment_counter() {
counter++;
return(counter);
}
|
threadprivate 和 private 的区别在于:前者声明的变量通常是全局范围内有效,而 private 只在自己的并行区域内有效。threadprivate 对应只能用于 copyin、copyprivate、schedule、num_threads 和 if 子句中。
default/shared 子句
如果我们想让不同的 section 共同编辑一个变量,就要用 default(shared) 声明, 如果是 default(none),则线程中用到的变量必须指明是私有的还是共享的,毕竟如果不说明参数,很容易造成误会。
reduction 规约子句
这个就是我们在 MPI 中用到的规约子句:
1
2
3
4
5
6
| int i, sum = 100;
#pragma omp parallel for reduction(+: sum) {
for ( i = 0; i < 1000; i++ ){
sum += i;
}
printf( "sum = %ld\n", sum);
|
上面的程序为每个线程执行规约加法操作,其中 + 为规约操作类型,sum 为规约变量(reduction 操作类型与 reduction 变量)。